
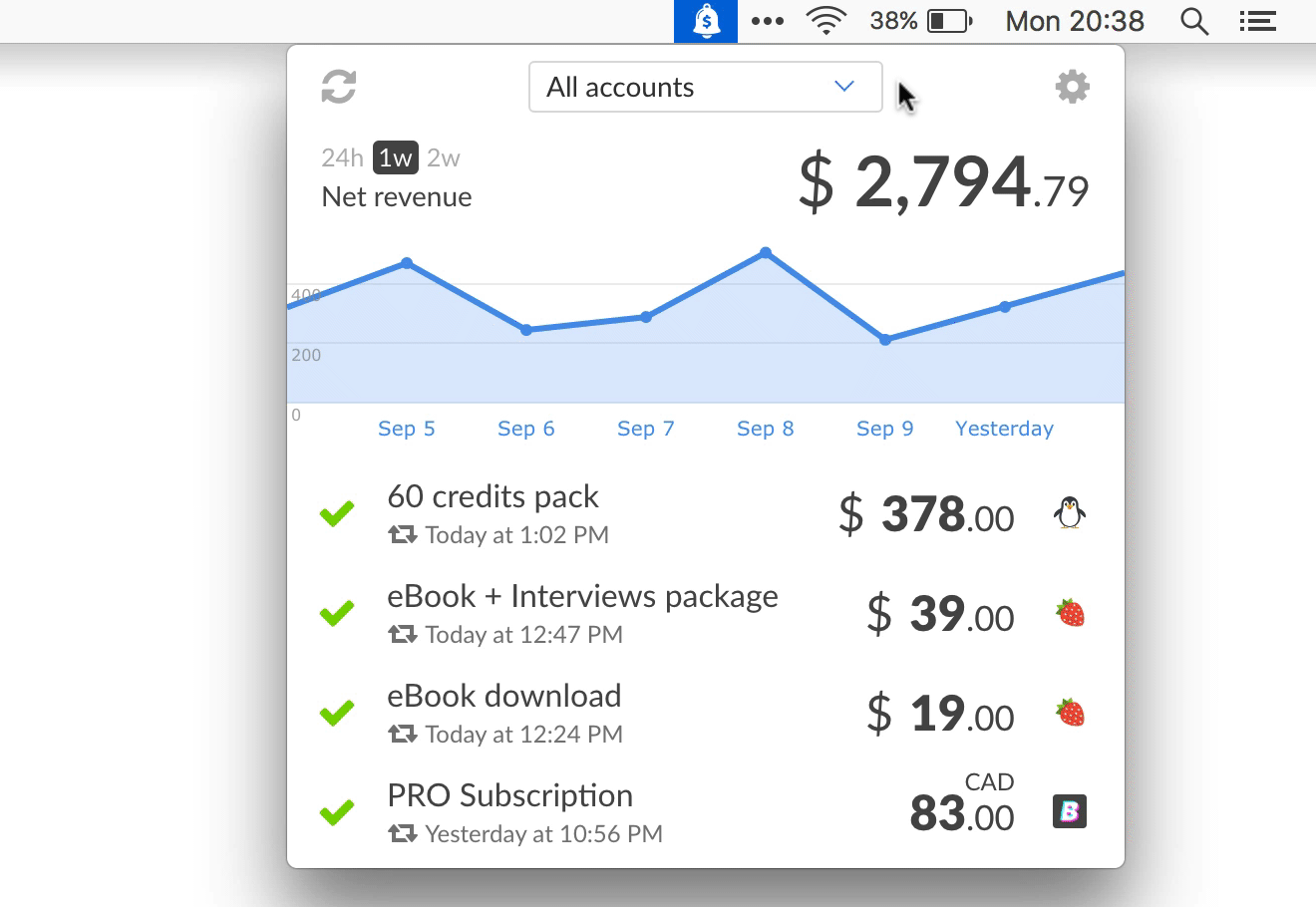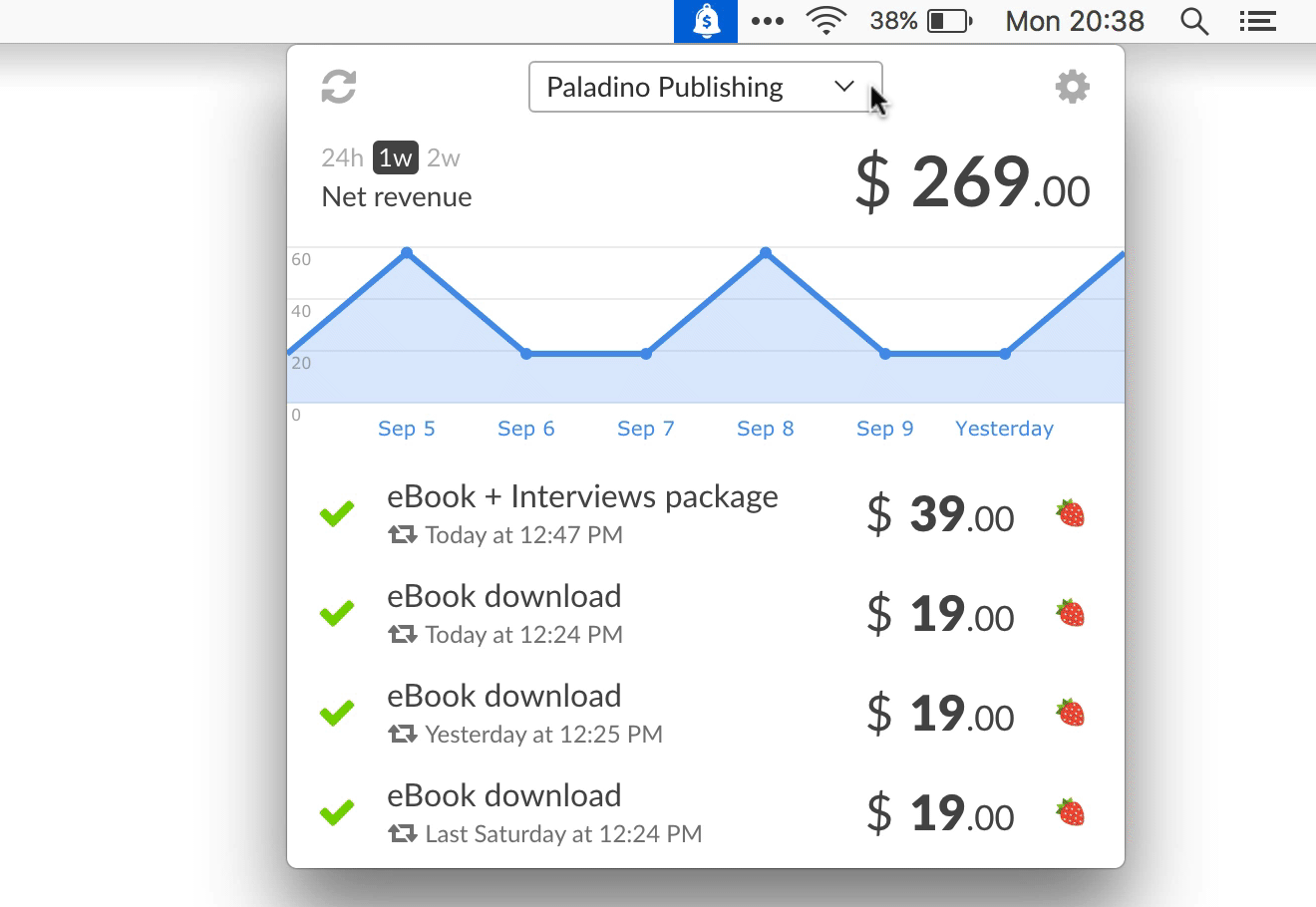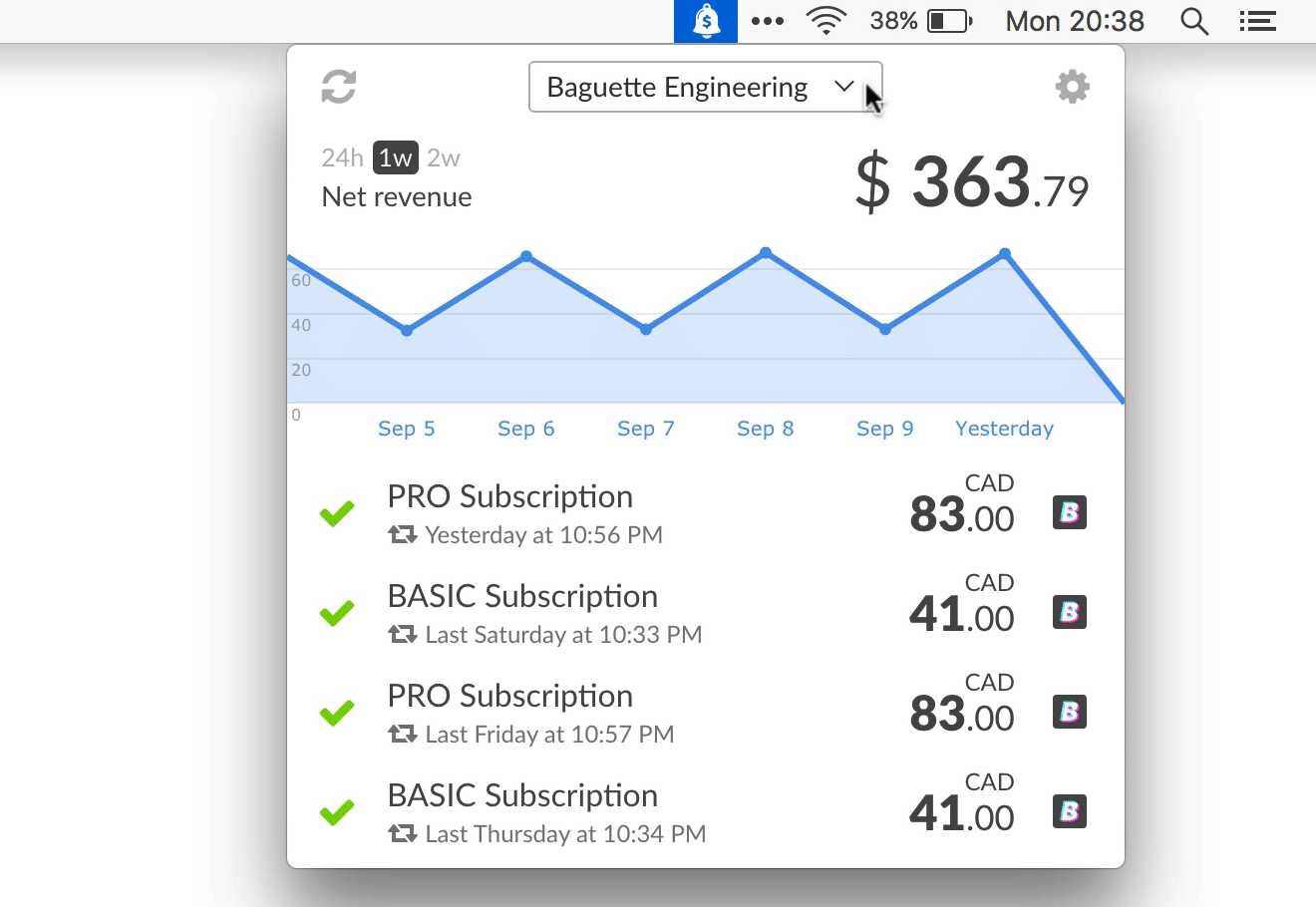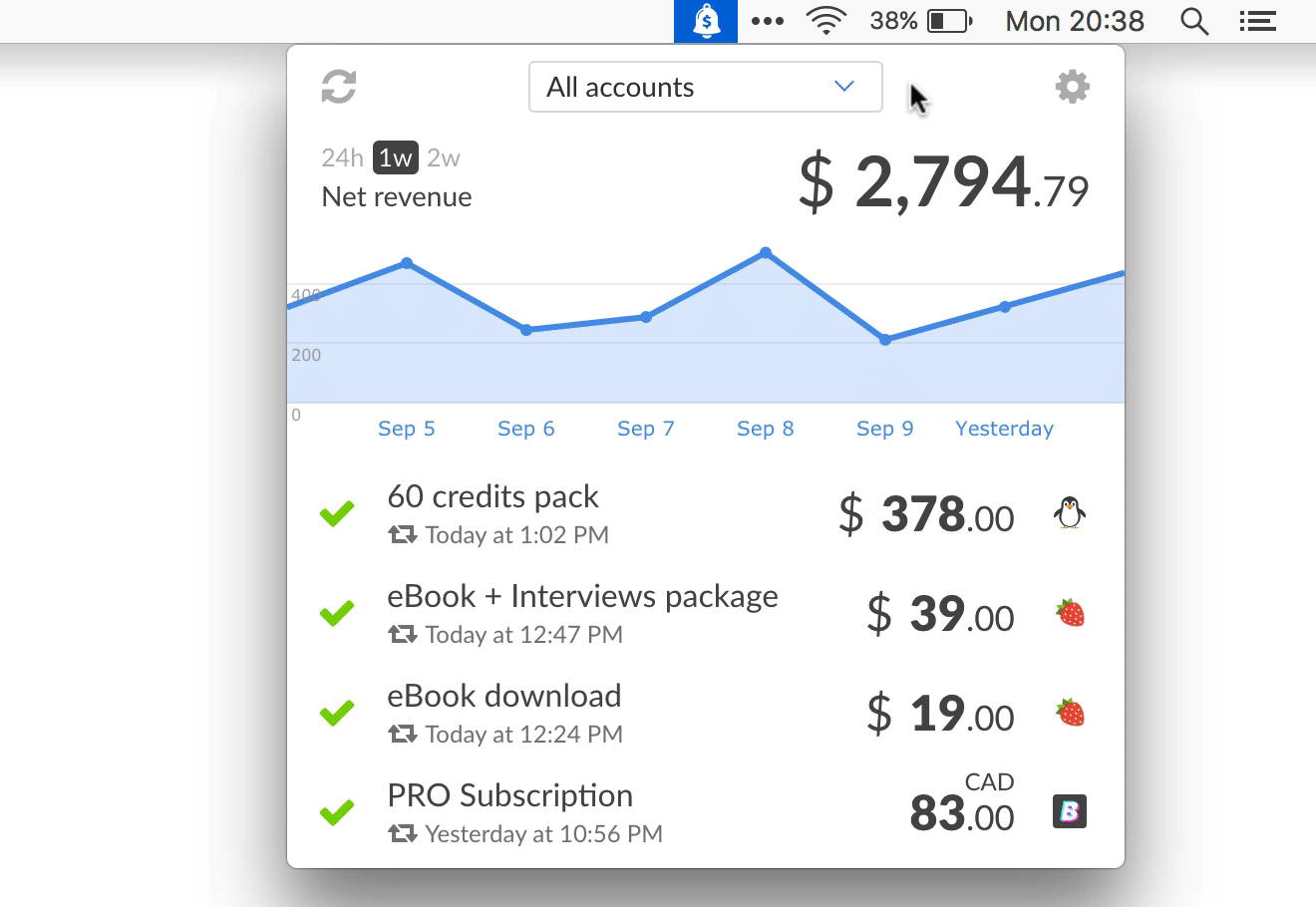
If we can compute the derivative of a function, we know in which direction to proceed to minimize it. Derivatives are used to decide whether to increase or decrease the weights to increase or decrease an objective function.
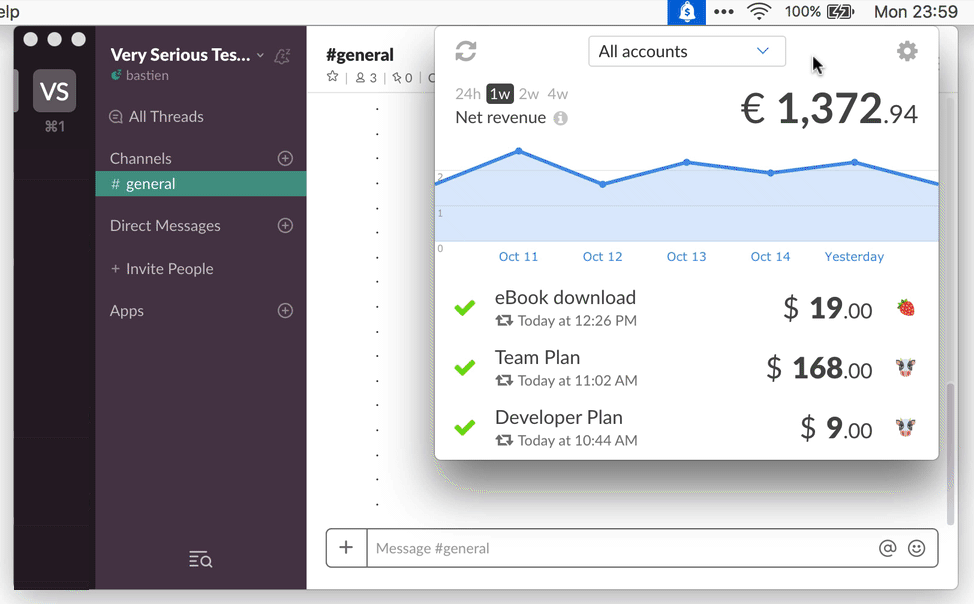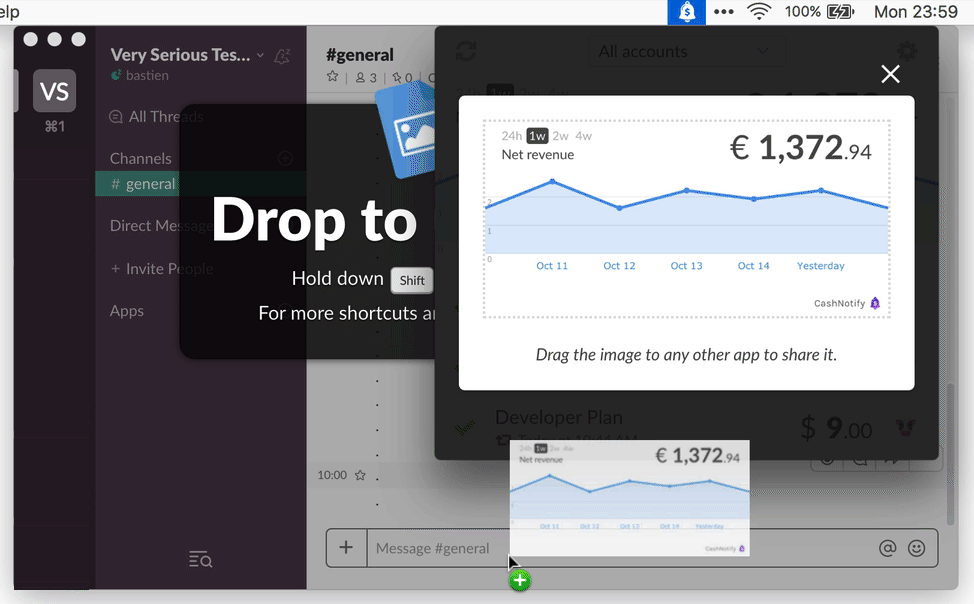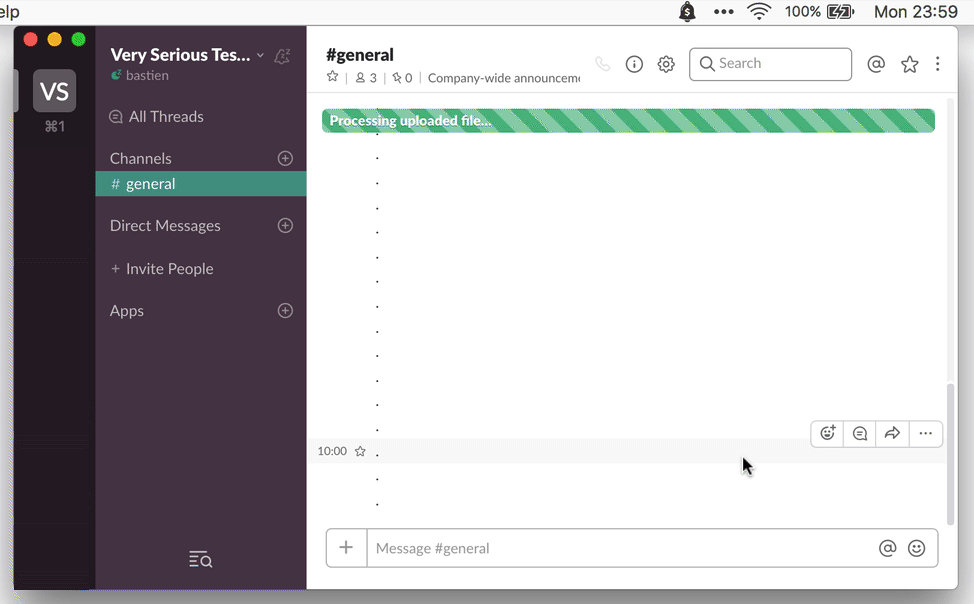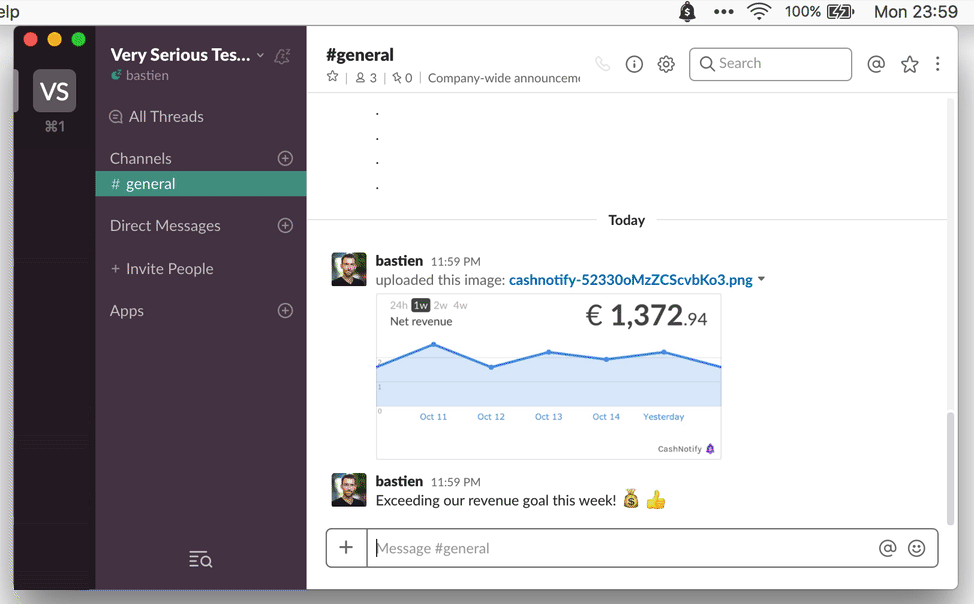
Machine learning uses derivatives in optimization problems. So don’t worry friends, just stay with me… it’s kind of intuitive! I assume that the readers are already familiar with calculus but will provide a brief overview of how calculus concepts relate to optimization here. In machine learning, the cost function is a function to which we are applying the gradient descent algorithm. So in gradient descent, we follow the negative of the gradient to the point where the cost is a minimum. Suppose we have a function with n variables, then the gradient is the length-n vector that defines the direction in which the cost is increasing most rapidly. So we can use gradient descent as a tool to minimize our cost function. Gradient descent is a method for finding the minimum of a function of multiple variables. For example, our cost function might be the sum of squared errors over the training set. Well, a cost function is something we want to minimize. We might argue that if the cost function and gradient descent are both used to minimize something then what is the difference and can we use one instead of the other?
It is not possible to decrease the value of the cost function by making infinitesimal steps.Ī global minimum is a point that obtains the absolute lowest value of our function, but global minima are difficult to compute in practice. A local minimum is a point where our function is lower than all neighboring points.


 0 kommentar(er)
0 kommentar(er)
